평균시간선택알고리즘

정렬되지 않은 배열에서 k번째로 작은 값을 찾는 알고리즘
선택에 목적이 있다. (정렬이 아님)
퀵정렬에서 파생되었다.

평균적으로 선형시간이 소요되는 알고리즘(k번째 작은 수 찾기)

입력된 정렬되지 않은 배열과 선택할 index번호(k번째)를 받는다
(퀵정렬) 배열에서 pivot을 정한다 (pivot을 선택하는 방법은 다양하다.)
pivot을 기준으로 분할된 두부분중 k번째 작은값의 위치가 있는 부분을 대상으로 다시 퀵정렬 실행
재귀적으로 반복하여 값을 찾는다.

select(A,left,right,k)
{
	if(left=right) then return A[left];  //원소가 하나뿐인 경우. k는 반드시 1
    pivot = partition (A, left, right);  //pivot에 피봇 인덱스값 저장
    i = pivot-left+1; 					//pivot이 i번째 작은 원소임을 의미
    if(k<i) then return select(A, left, pivot-1, k);	//왼쪽 그룹으로 범위를 좁힘
    else if(i=k) then return A[pivot];					//pivot이 바로 찾는 원소
    else return select(A, pivot+1, right, k);
}

평균 수행 시간은 존재할 수 있는 K의 모든 최대의 경우의 평균을 통해 시간 복잡도를 계산한다.

- 평균 시간복잡도 : $$O(n)$$

최악의 경우 : 분할할 때마다 그룹이 항상 1:n-1개의 원소로 분할 되고, 선택되는 그룹이 항상 n-1개 원소를 가진 그룹인 경우

- 최악 시간복잡도 : $$O(n^2)$$

분할의 균형에 영향을 받는다.!

최악의 경우에도 선형 시간이 소요되는 알고리즘

최악의 경우 분할의 균형이 어느정도 보장되도록 함으로써 수행시간이 이 되도록 한다.
분할의 균형을 유지하기 위한 오버헤드가 지나치게 크면 안된다.

linearSelect(A,p,r,i)
//배열A[p...r]에서 i번째 작은 원소를 찾는다.
{
	1. 원소의 총 수가 5개 이하이면 원하는 원소를 찾고 알고리즘을 끝낸다. (상수시간 간주)
	2. 전체 원소들을 5개씩의 원소를 가진 n/5 개의 그룹으로 나눈다.
	3. 각 그룹에서 중앙값을 찾는다. 이렇게 찾은 중앙값들을 m1, m2, ...,m(n/5)라고 한다.
	4. m1, m2, ...,m(n/5) 들의 중앙값 M을 재귀적으로 구한다. [call linearSelect()]
	5. M을 기준원소로 삼아 전체 원소를 분할한다.
	6. 분할된 두 그룹 중 적합한 쪽을 선택하여 단계 1-6을 재귀적으로 반복한다. [call linearSelect()]
}

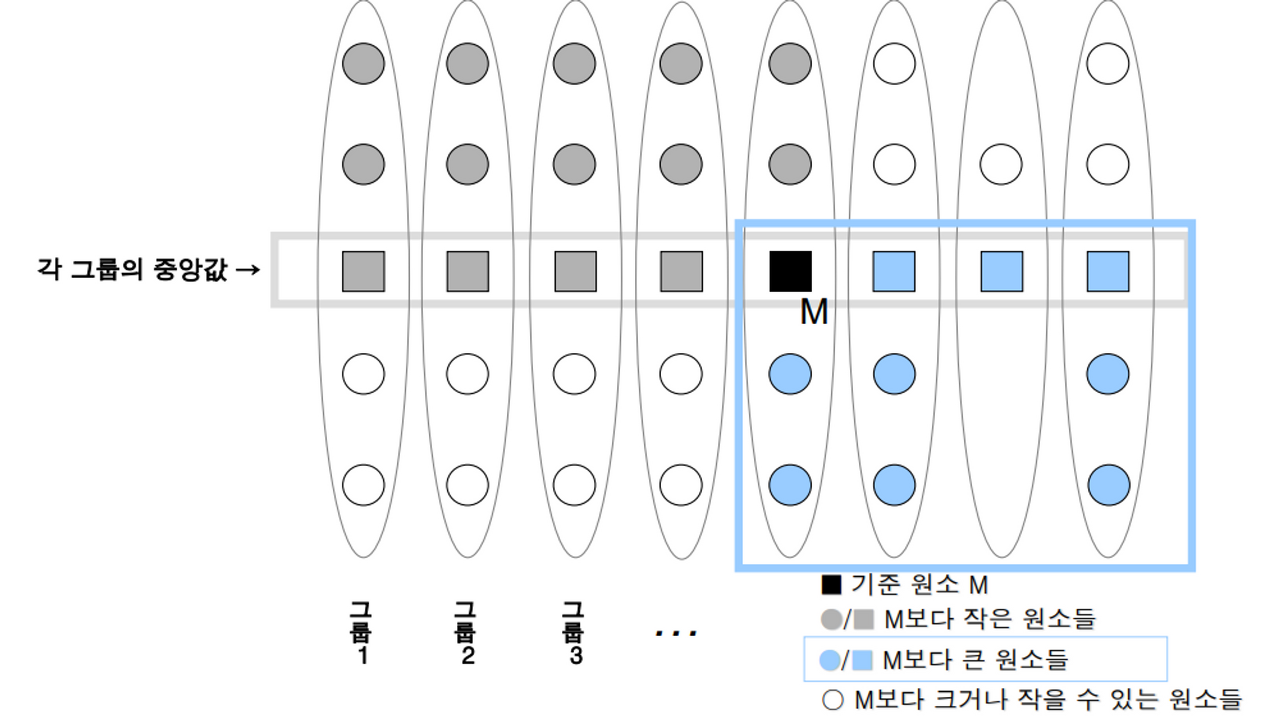
→ M을 pivot 값으로 정한다.

→ 왼쪽 상단(회색)과 오른쪽 하단(하늘색)이 M보다 큼/작음이 확실한 원소들의 존재로 인해 분할 할 때 양쪽 그룹의 비율이 일정 수준 이상으로 보장된다.

평균 시간 선택 알고리즘

- 중앙값(pivot 값)을 어떻게 잡는지에 따라 선택 알고리즘의 종류가 결정된다.

1. 평균적으로 선형시간이 소요되는 알고리즘 -> Quick Select Algorithm

2. 최악의 경우에도 선형시간이 소요되는 알고리즘 -> Median of Median Algorithm

단, Median of Median 알고리즘의 최악의 경우 시간복잡도가 O(n)으로 우수함에도 사용하지 않는 이유는 실질적으로 많은 메모리와 오버헤드의 이슈(5개 이하에 대한 평균값을 구하는 무한히 많은 원소를 상정)으로 대게의 경우 이보다는 random하게 구하는 것이 가장 효율적으로 알려져 있다. Randomized Quick Select Algorithm으로도 불리며, 이론적인 최악의 시간 복잡도는 O(n^2)이지만 실제 Qucik Select Algorithm보다 실질적 중앙값을 찾을 확률이 높아, worst case의 시간 복잡도가 발생할 가능성이 현저히 낮은 알고리즘이다.